Predictable
Table of contents
Enumeracion
Iniciamos con un escaneo de nmap donde encontraremos los puertos, 22 (SSH) y 1111:
nmap -sS -n -Pn --open -p- 172.17.0.2
sS: haga un TCP SYN Scan el cual hace un escaneo sigiloso sin completar las conexiones TCP, responde con un SYN/ACK si el puerto esta abierto
n: para que no haga resolucion DNS y tarde menos el escaneo
Pn: para evitar el descubrimiento de hosts
open: para que solo muestre los puertos abiertos
-p-: para que escanee todo el rango de puertos
PORT STATE SERVICE
22/tcp open ssh
1111/tcp open lmsocialserver
Al realizar otro escaneo para obtener mas informacion sobre la version y servicio, nos damos cuenta en el puerto 1111 esta corriendo una aplicacion es flask
nmap -sCV -p22,1111 172.17.0.2
- sCV: Lanza script para enumerar el servicio y obtiene informacion sobre la version del servicio
1111/tcp open http Werkzeug httpd 3.0.3 (Python 3.11.9)
|_http-title: Predictable
|_http-server-header: Werkzeug/3.0.3 Python/3.11.9
Service Info: OS: Linux; CPE: cpe:/o:linux:linux_kernel
1111 - HTTP
El revisar el puerto 1111, veremos que tenemos una sitio web donde nos muestran 99 numeros y nos pide adivinar el siguiente (numero 100), ademas nos muestra la semilla anterior que la que se usa en la generacion de numeros actual, y por ultimo, cada vez que ingresamos un numero mal o recargamos la pagina, la semilla se actualiza, eso es interesante por que mientras no hagamos nada, la semilla sera la misma.
Si presionamos Ctrl + u, veremos que en unos comentarios saldran partes del codigo fuente de la aplicacion:
class prng_lcg:
m =
c =
n = 9223372036854775783
def __init__(self, seed=None):
self.state = seed
def next(self):
self.state = (self.state * self.m + self.c) % self.n
return self.state
...
# return int
def obtener_semilla():
return time.time_ns()
def obtener_semilla_anterior():
return obtener_semilla() - 1
...
if 'seed' not in session:
session['seed'] = obtener_semilla()
gen = prng_lcg(session['seed'])
...
gen = prng_lcg(session['seed'])
semilla_anterior = obtener_semilla_anterior()
Tenemos poca informacion, pero la necesaria para resolver el desafio, primero vemos que el PRNG que usa es la tipica implementacion de LCG (Linear Congruential Generator), despues se define una funcion de nombre “obtener_semilla” la cual obtiene la semilla con base el tiempo actual hasta segundos, otra funcion de nombre “obtener_semilla_anterior”, la cual simplemente resta - 1 a la semilla original, y esta es la semilla que muestra el sitio web. Despues se verifica si la “seed” no esta especificada en la sesion del usuario, en caso de que no, se llama a la funcion “obtener_semilla” para almacenar esa semilla en “seed”. Posteriormente usa la semilla que esta en “seed” para inicializar el prng (gen = prng_lcg(session[“seed”])), por ultimo asigna la variable “semilla_anterior” el valor de retorno de la funcion “obtener_semilla_anterior”. Con todo lo que tenemos hasta ahora sabemos que:
- Usa LCG como PRNG
- La semilla es el tiempo actual hasta segundos
- La semilla que se muestra en la web es la semilla original - 1
- La semilla se actualiza cada que ponemos un numero mal y recargamos la pagina
- Tenemos que adivinar el numero 100
- La semilla no cambia mientras no hagamos nada en el sitio web
Explotando LCG
Si volvemos a ver el codigo de LCG, nos daremos cuenta que nos faltan los valores de m (multiplicador) y c (incremento). Eso no es un problema sabiendo que LCG esta dado de acuerdo a esta ecuacion
- Donde Xn es la semilla
- X1, X2, X3… son lo numeros pseudoaleatorios
- a, c, m son constantes
Simplemente conociendo el valor de una de las constantes, podemos despejar esa ecuacion para obtener los valores de las demas constantes (incremento y multiplicador), en nuestro caso solo tenemos el valor del modulo (9223372036854775783) y tenemos una lista de numeros aleatorios generados, asi que podriamos ir resolviendo esto asi:
Calcular el multiplicador (m) Dado a que tenemos numeros generados consecutivamente, tenemos las siguientes ecuaciones:
x1 = (x0 * m + c) mod n
x2 = (x1 * m + c) mod n
Y podemos derivarlas para c:
c ≡ x1 - x0 * m mod n
Que esto nos indica que c es congruente con x1 - x0 por m y modulo n, osea que la diferencia de x1 - x0, obtiene el mismo residuo cuando de dividen por n. Y la siguiente ejecucion seria:
c ≡ x2 - x1 * m mod n
Que es lo mismo que la anterior pero con x2 - x1.
Ahora podemos igualar estas dos ecuaciones para c:
x1 - x0 * m ≡ x2 - x1 * m mod n
Simplificando obtendriamos:
x1 - x2 ≡ -m (x1 - x0) mod n
Ahora multiplicaremos ambos lados por -1:
x2 - x2 ≡ m (s0 - s1) mod n
Con esto ya podemos resolver m:
m ≡ x2 - x1/x0 - x1 mod n
Sin embargo para resolver x2 - x1/x0 - x1 mod n, necesitamos el inverso modular de (x0 - x1) mod n
Para calcular el inverso modular podemos decir que el inverso modular de a mod n es un numero a¹ tal que:
a * a⁻¹ ≡ 1 mod n
Ahora, para encontrar el inverso modular lo podemos hacer usando el algoritmo extendido de Euclides. Tomando en cuenta que dados numeros a y b, tenemos que encontrar el maximo comun divisor (gcd) y los coeficientes de Bezout, “x, y” tales que:
ax + by = gcd(a, b)
Donde si gcd(a, b) = 1, entonces x es el inverso modular de a mod b,Ahora ya simplemente podemos calcular c(incremento):
c ≡ x1 - x0 * m mod n
Ahora debemos de pasar todo lo anterior a python u otro lenguaje y ya, el cual el codigo final quedaria asi:
# calcula el máximo común divisor de a y b, junto con los coeficientes de la identidad de Bezout
def egcd(a, b):
if a == 0:
return b, 0, 1
else:
g, y, x = egcd(b % a, a)
return g, x - (b // a) * y, y
# devuelve el inverso modular de a mod m, si existe
def modinv(a, m):
g, x, y = egcd(a, m)
if g != 1:
raise Exception('No existe')
else:
return x % m
def crack_lcg(states, modulo):
x0, x1, x2 = states[0], states[1], states[2]
# calcular el multiplicador
inverso = modinv(x0 - x1, modulo)
multiplicador = (inverso * (x1 - x2)) % modulo
# calcular el incremento
incremento = (x1 - x0 * multiplicador) % modulo
return modulo, multiplicador, incremento
states = [3500105493060415586, 3409125950685693468, 2405670402399141717] #primeros 3 numeros generados del sitio web
modulo = 9223372036854775783
modulo, multiplicador, incremento = crack_lcg(states, modulo)
print("modulo:", modulo)
print("multiplicador:", multiplicador)
print("incremento:", incremento)
Si lo corremos podemos ver que obtenemos los valores del multiplicador e incremento
modulo: 9223372036854775783
multiplicador: 81853448938945944
incremento: 7382843889490547368
Ahora podemos aplicar el mismo codigo de LCG que se usa en la web y generar el numero 100
class prng_lcg:
m = 81853448938945944 # multiplicador
c = 7382843889490547368 # incremento
n = 9223372036854775783 # modulo
def __init__(self, seed):
self.state = seed
def next(self):
self.state = (self.state * self.m + self.c) % self.n
return self.state
def lcg():
gen = prng_lcg(1719346377 + 1)
for numero in range(100):
print(gen.next())
lcg()
Si lo ejecutamos nos generara 100 numeros, y el numero 100 es el que ingresaremos en la web y veremos que obtenemos unas credenciales:

Pyjail escape
Si ingresamos por SSH nos daremos cuenta que estamos con una “shell” de python, la cual toma la idea es una python jail, donde tenemos bloquedas ciertas palabras
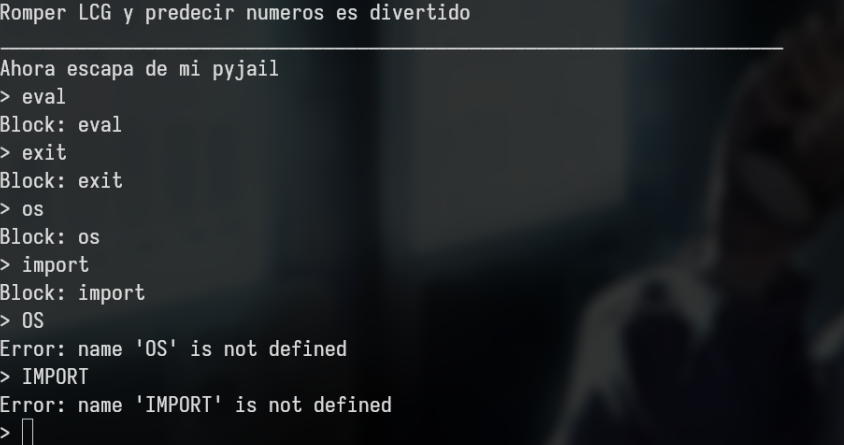
Tambien si vemos, cuando ingresamos “OS” con mayuscula, no lo bloquea, eso quiere decir que podemos manejar la mayusculas. En este tipo de desafios normalmente debemos de jugar con las funciones incorporadas de python, es decir, las builtins, es tan simple como ingresar “builtins.dict” y podremos ver diversas clases

Como el objetivo final es escapar y comunmente es spawneando una shell, podemos usar el metodo lower(), ya que no podemos usar minusculas, e importar el modulo os para ejecuctar un comando, como se ve en el siguiente ejemplo

Ahora solo falta cambiar el “id” por bash y conseguir una shell de bash

Escalada
Si mostramos los permisos a nivel de sudoers, podremos ver que podemo ejecutar el archivo “shell” como root sin contraseña
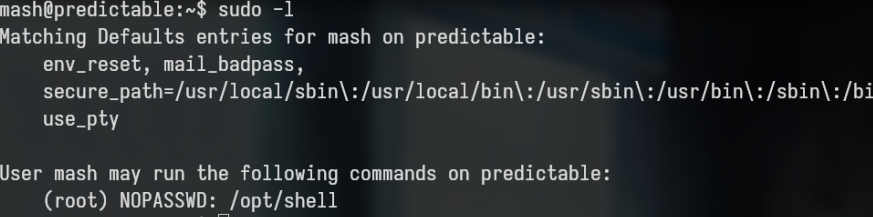
Al ejecutarlo veremos que nos pide un input y con la opcion -h nos da una pista que dice
¿Sabias que EI_VERSION puede tener diferentes valores?. radare2 esta instalado
EI_VERSION especifica el numero de version del encabezado ELF, el cual por defecto esta en el byte 6 o con desplazamiento de 6 bytes de e_ident, actualmente solo existe una sola version de ELF que se define en EV_CURRENT (1)
Para el reversing hay que empezar sabiendo que el puntero de argv se copia a s2

Mas abajo podemos ver que la direccion del puntero s2 se mueve rax y se incrementa en 8 (lo cual estaria apuntando al segundo elemento de argv), esto es asi por que el tamaño del puntero en x86_64 es de 8 bytes o 64 bits, posteriormente mueve el valor de 8 bytes almacenado en la direccion de memoria a la que apunta rax, posteriormente viene una parte importante, con movzx movemos con cero extendido el byte de la direccion a la que apunta rax al registro eax, esto ocasiona que los bits no usados se pongan en 0, luego se compara con 0x30 o 0 en ASCII, es importante esta ultima parte por que basicamente solo se esta comprobando si el primer de nuestra entrada es 0, sin importar lo demas

Pero si lo corremos indicando nuestro input es 0, aun asi fallara, por que existe otra comprobacion:

Podemos ver varias, cosas, vemos que con la funcion fopen se esta abriendo el mismo archivo (shell), esta operacion regresa el “fd” para hacer referencia a ese archivo en otras partes del programa, y despues usa “fseek” indicandole como parametro el “fd”, y dos numeros, 0 y 6, estos estos numeros indican por donde empezar a mover el puntero de posicion del archivo y cuantos bytes mover el puntero del archivo, entonces podemos decir que nos estamos moviendo el sexto byte en el archivo, al final se llama a la funcion fread con los numeros 1, 1, que representan el tamaño a leer del archivo y cuantos bytes de ese tamaño, por lo que solo estariamos leyendo un solo byte desde la posicion actual (que seria la posicion a la que nos movimos usando fseek), y por ultimo se compara ese valor con 1. Si regresamos a lo de EI_VERSION sabemos que esta en el byte 6 del encabezado ELF, pues este byte puede tomar valores de entre 0-255 y 0x00 y 0xff, que estos valores representan 0 para ninguna version ELF, y 1 para la actual y unica version ELF (EV_CURRENT (1)), asi que tomando en cuenta que el valor que estamos leyendo con fread se esta comparando con 1, podemos decudir que se esta comparando si el archivo ELF esta usando la unica y actual version ELF, ahora es mas sencillo, por que podemos sobrescribir el desplazamiento con lo que queramos que no sea 0x01, esto con el fin de pasar la comprobacion que se hace (cmp al, 1) y ejecutar el programa pasandole un 0, para hacer eso, debemos de parchear el binario usando r2 con la opcion -w
Si seguimos los pasos abremos obtenido la shell como root, ya que el binario ejecutaba /bin/bash si le pasabamos la respuesta correcta.
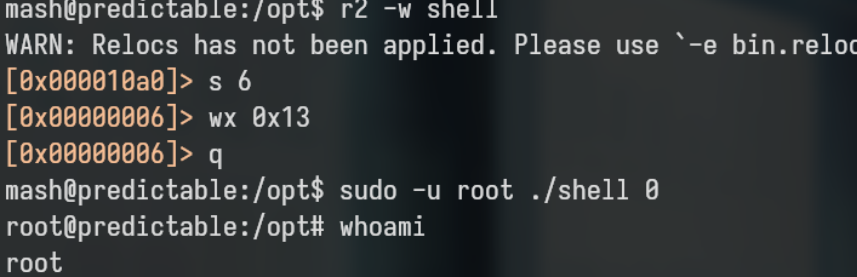
Eso ha sido todo, gracias por leer :D
